Probabilités et statistiques

• Théorie de l'échantillonnage = Étude des liaisons existant entre une population et les échantillons de cette population, prélevés par sondage.

  • Méthodes d'échantillonnage : ensemble des méthodes permettant de réaliser un sondage (de prélever un échantillon de données) au sein d'une de manière à reproduire un échantillon aussi représentatif que possible de cette population.

  • Évaluation de ces méthodes : le système d'échantillonnage sera jugé d'après la qualité des approximations des paramètres de la population, calculées

    sur l'échantillon prélevé . Pour cela, on étudiera la loi des caractéristiques classiques d'un échantillon (moyenne arithmétique , variance empirique,...)

• Les méthodes empiriques : les plus utilisées par les instituts de sondage. Leur précision ne peut pas être calculée et leur réussite dépend de l'expertise des enquêteurs.

  • Échantillonnage sur la base du jugement : Échantillon prélevé à partir d'avis d'experts, qui connaissent bien la population et sont capable de dire quelles sont les entités représentatives.

    Pbme: l'avis des experts est subjectif.

  • Échantillonnage par la méthode des quotas : Échantillon prélevé librement à condition de respecter une composition donnée à l'avance

    (sexe, âge, CSP,...).

    Pbme : repose sur la pertinence des catégories retenues

• Les méthodes aléatoires : Reposent sur le tirage au hasard d'échantillons et sur le calcul des probabilités

  • Échantillonnage aléatoire simple : On prélève dans la population, des individus au hasard, sans remise : tous les individus ont la même probabilité d'être prélevés, et ils le sont indépendamment les uns des autres.

  • Échantillonnage aléatoire stratifié : Suppose que la population soit stratifiée, i.e. constituée de sous-populations homogènes, les strates. (ex : stratification par tranche d'age). Dans chaque strate, on fait un échantillonnage aléatoire simple, de taille proportionnelle à la taille de strate dans la population (échantillon représentatif). Les individus de la population n'ont pas tous la même probabilité

    d'être tirés. Nécessite une homogénéité des strates. Augmente la précision des estimations.

  • Échantillonnage par grappe : on tire au hasard des grappes ou familles d'individus, et on examine tous les individus de la grappe (ex: on tire des

    immeubles puis on interroge tous les habitants). La méthode est d'autant meilleure que les grappes se ressemblent et que les individus d'une même grappe sont différents, contrairement aux strates.

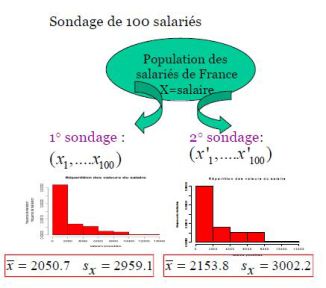
Quelle que soit la technique d'échantillonnage utilisée, le contenu du jeu de données prélevé varie d'un sondage à l'autre

On pourrait répéter le sondage un grand nombre de fois, on obtiendrait la plupart du temps une répartition différente des valeurs

prélevées.

Le résultat d'un sondage est aléatoire

• Objectif : étudier la loi des statistiques classiques de l'échantillon aléatoire (les distributions d'échantillonnage), en fonction de la distribution de la variable parente, lorsque la taille de l'échantillon augmente.

• Définition d'une statistique = variable aléatoire, définie comme une fonction de l'échantillon aléatoire

  $S=f(X_1,\cdots ,X_n)$

  Lorsque$(X_1,\cdots ,X_n)=(x_1,\cdots ,x_n)$ la réalisation de S vaut $s=f(s_1,\cdots ,s_n)$

  Exemples de statistiques : Moyenne empirique de l'échantillon, variance

  empirique, covariance empirique, fonction de répartition,.....

• Moyenne empirique : $\overline{x}=\frac{1}{n}\sum _{i=1}^n{x}_i$

• Variance "empirique" : $s^2=\frac{1}{n}\sum _{i=1}^n{(x_i-\overline{x})}^2$

• Moment "empirique"