Probabilités et statistiques

Etude Statistique = étude des caractéristiques (variables statistiques) d'un ensemble

d'objets (population, composée d'individus) .

• Recensement : les valeurs des variables sont disponibles sur l'ensemble de la population $\Rightarrow$statistique descriptive (pas besoin de stat inférentielle)

Ex : Recensement de la population française, notes obtenues par tous les

candidats à un examen, salaires de tous les employés d'une entreprise, $\cdots$

Pbme : coûteux, long, impossible (population infinie), mesures

destructrices (ex : tests en vieillissement accélérés)

• Sondage :

• On n'étudie qu'une partie de la population : un échantillon. Les méthodes permettant de réaliser un échantillon de bonne qualité (sui ressemble à la population dont il est issu) sont étudiées en théorie de l'échantillonnage.

• On cherche alors à extrapoler à la population entière les propriétés mises en évidence sur l'échantillon $\Rightarrow$statistique inférentielle

• La population est considérée comme infinie (très grande )

• les variables statistiques qui la décrivent peuvent être considérées comme des v.a.

La valeur prise par la variable statistique$X$  pour un individu donné de la population ne peut pas être déterminée a priori et dépend d'un grand nombre de paramètres : On peut considérer sa valeur comme fonction du résultat d'une expérience aléatoire

Ex : répartition des salaires des salariés dans la population française : série$(x_1,\cdots ,x_n)$, vue comme n réalisations de la variable aléatoire $X$=salaire

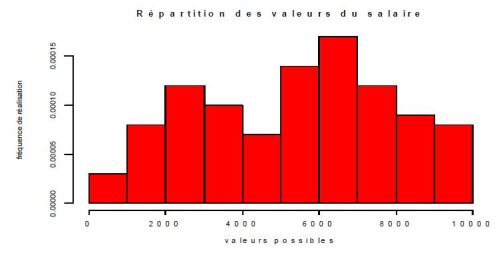
• La répartition des valeurs de ces variables sont caractérisées par des lois de probabilités

  La répartition d'une variable statistique $X$sur la population est décrite par une loi de probabilité

  Ex: si l'on suppose que les salaires sont soumis à un grand nombre de petites fluctuations d'origines diverses, $X$ suit une loi normale tronquée à zero.

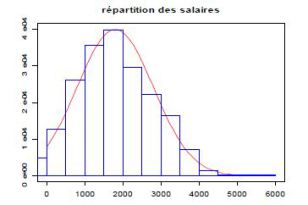
• caractérisée par une densité de probabilité ( $X$continue )ou une séquence de fréquences relatives à chacune de ses valeurs ($X$ discrète)

• possédant des caractéristiques ($E(x),V(x)$, autres paramètres résumant la distribution.)

  Les variations simultanées de deux ou plusieurs variables statistiques sont décrites par une loi jointe

  • caractérisée par une densité jointe (variables continues) ou une séquence des fréquences jointes (variables discrètes).

    • Ex : les variations simultanées du salaire et de l'age des salariés pourront être décrites par une fonction de densité jointe $f(x,z)$.

  • possédant différentes caractéristiques, par exemple un vecteur espérance, une matrice de variance covariance , un coefficient de corrélation linéaire

• Ces lois de probabilités sont généralement

  • Totalement Inconnues : nous ne connaissons rien de la loi - problème de statistique inférentielle non-paramétrique

  • Partiellement inconnues : nous connaissons la famille à laquelle appartient la loi (sa forme) mais pas ses ou un certain nombre de ses

  paramètres (Ex : X obéit à une loi normale, mais on ne connaît ni son espérance ni sa variance – problème de statistique inférentielle paramétrique