Introduction
S'intéresser à la sémantique de la logique propositionnelle, c'est déterminer la valeur de vérité d'un énoncé, c'est-à-dire d'une formule. On parle de l'interprétation d'une formule : il s'agit plus concrètement d'affecter une valeur vraie ou fausse à chacune des variables propositionnelles qui la compose. Pour une formule à n variables, il y a 2n mondes possibles.
Valuation : On appelle valuation, ou L-Modèle, d'un ensemble de variables propositionnelles v ⊆ v(L), une fonction m de v(L) dans {T, F} (m : v(L) → {T, F}).
v (﹁X)= ﹁v(X),
v(x ∧ Y)= v(x) ∧ v(Y),
v(x ∨ Y)= v(x) ∨ v(Y),
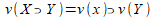 .
.
Interprétation : Une valuation appliquée à une formule dans laquelle est dite interprétation. soit la formule F = (a ∧ b) ∨ ¬b → ¬a, {m(a) = T, m(b) = F} est une interprétation de F.
Modèle d'une formule : Une interprétation I est un modèle d'une formule A si elle est vraie (si elle vaut T).






