Correspondance entre bases
Conversion d'un nombre en base b à un nombre en base 10. Il suffit d'utiliser la méthode polynomiale.
Pour passer d'un nombre en base 10 à un nombre en base b, nous pouvons utiliser deux méthodes :
La méthode des soustractions : Pour utiliser cette méthode, on doit déterminer en premier lieu, les valeurs successives 2i (i=0,...,n), on déterminera ensuite, entre quelles valeurs successives de 2i se situe le nombre à convertir. La borne inférieure est alors soustraite au nombre. On procède de la même manière avec le reste obtenu, jusqu'à ce que l'on obtienne zéro comme reste de la soustraction.
la valeur binaire sera 1 à la position du poids utilisé dans la soustraction, et 0 à la position des poids non utilisés.
La méthode des divisions : Pour convertir un nombre de la base 10 vers une base B quelconques, il faut faire des divisions successives par B et retenir à chaque fois le reste jusqu'à l'obtention à un quotient inférieur à la base B, dans ce cas le nombre s'écrit de la gauche vers la droite en commençant par le dernier quotient allant jusqu'au premier reste.
Correspondance entre binaire et décimal (transcodage)
Conversion d'un nombre binaire en décimal. Il suffit de faire la somme des poids de chaque bit à 1.
Exemple : Méthode des soustractions
Conversion d'un nombre décimal en binaire (exemple : N = 172).

Méthode des soustractions successives.
Exemple : Méthode des divisions
Conversion d'un nombre décimal en binaire (exemple : N = 172).
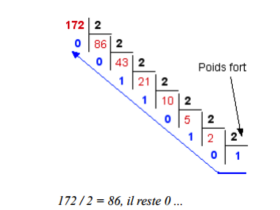
Méthode des divisions successives.
Correspondance entre binaire et hexadécimal
La conversion du binaire en hexadécimal est très simple, c'est d'ailleurs la raison pour laquelle nous utilisons cette base. Il suffit de faire correspondre un mot de quatre bits
Suite Hexa | Suite Binaire | Suite Hexa | Suite Binaire |
|---|---|---|---|
0 | 0000 | 8 | 1000 |
1 | 0001 | 9 | 1001 |
2 | 0010 | A | 1010 |
3 | 0011 | B | 1011 |
4 | 0100 | C | 1100 |
5 | 0101 | D | 1101 |
6 | 0110 | E | 1110 |
7 | 0111 | F | 1111 |
Exemple :
Conversion d'un mot de 16 bits entre binaire et hexadécimal :
Soit le nombre (4D7F) en base 16, trouvez son correspondant en base 2 ?
(4D7F) 16 = (0100110101111111)2

Exemple de correspondance de la base 16 vers la base 2.
Correspondance entre le binaire et l'octal
La conversion entre le système binaire et octal est simple. Il suffit de regrouper de bits en des sous ensembles de trois bits puis remplacé chaque groupe par un symbole de la base 8 (voir la table ci-dessous).
Symbol octal | Suite binaire |
|---|---|
0 | 000 |
1 | 001 |
2 | 010 |
3 | 011 |
4 | 100 |
5 | 101 |
6 | 110 |
7 | 111 |
Exemple :
Le nombre binaire (001 010 011 001)2 = (1231)8.