Opérations arithmétiques en binaire
Addition
L'addition est réalisée bit à bit. Il faut retenir[1] :
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 0 avec retenue de 1.
Exemple :
Donner l'addition des deux nombres binaires suivants :
(10001101)2 et (1001)2.
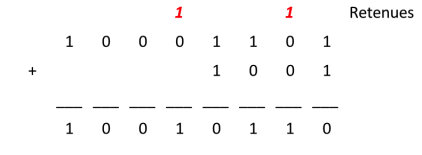
Exemple d'addition de deux nombres binaires avec retenues.
Représentation d'un nombre binaire signé
On représente un nombre binaire signé sur 8 bits de la manière qui suit, où :
N0 à N6: sont les bits significatifs ;S: est le signe du nombre binaire (soitS=0le nombre est considéré comme positif ; soitS=1le nombre est considéré comme négatif);

Fondamental : le complément à 1 et le complément à 2
Pour déterminer l'opposé d'un nombre positif, on utilise la notation du complément à 2.
Exemple :
Donner l'opposé du chiffre 5 (-5) codé sur 8 bits.
(5)10 = (0 0000101)2
Le complément de 5 est ( 1 1111010)2.
Ajouter 1 au complément de 5 :
(1 1111010)2 + 1 = 1 1111011
En notation complément à 2 (-5)10 = 1 1111011(2)
Soustraction
Dans ce cours, nous verrons 2 méthodes de soustraction des nombres binaires.
La méthode du complément à 1 et addition ;
La méthode du complément à 2 et addition.
Exemple : Méthode 1 : Complément à 1 et addition
Soient les nombres binaires :
1101011101(2) ; 1011100111(2)
Le complément à 1 de 1011100111(2) = 0100011000
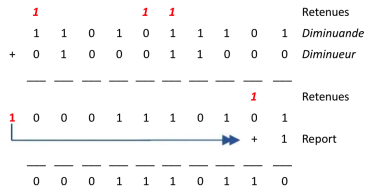
Remarque :
Si le diminueur est plus grand que le diminuande, il faut intervertir et affecter le résultat du signe moins.
Exemple : Méthode 2 : Complément à 2 et addition
25 -17 = ?(2)
25(10) = 00011001(2)
17(10) = 00010001(2)
-17(10) = 11101111(2)
Donc : 25 - 17 = 00011001(2) + 11101111(2)
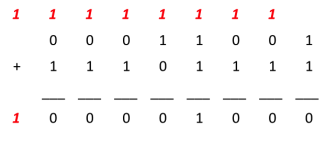
Remarque :
On remarque que le résultat est écrit en 9 bits, ce qui dépasse le format de 8 bits. Dans ce cas, on ignore le bit le plus à gauche appeler dépassement, et donc le résultat est : 00001000(2)
Multiplication
La multiplication en binaire est la même qu'en décimal.
Exemple :
Soient 1001(2) et 1011(2).
